Note: the article has been published originally on to my Medium account: https://medium.com/@ms.kaleia/tabu-search-gentle-introduction-46c479eb6525
Recently, I attended a course on discrete optimization on Corsera. One of the problems I was trying to solve is the Travelling Salesman Problem, the famous NP-Hard optimization problem. The course explained how to solve several real problems with several algorithms, one of them is Tabu Search. Today, in this post I will explain this algorithm and implement it using Python to solve the Travelling Salesman Problem TSP.
Hmm.. so what is Tabu search and where can I use it?
Tabu Search is a meta heuristic procedure for solving optimization problem designed to guide other methods to escape the trap of local minima. Tabu Search is used to find optimal and nearly optimal solutions for a wide range of classical and practical problems. From scheduling, to telecommunications, character recognition to neural networks. To avoid falling in a local minima, it uses a memory so it can remember moves and solutions that are already exploited. Also, it uses memory functions to allow searching strategies like intensify and diversify (will explain them soon).
Tabu Search can be used to guide other processes that uses a set of moves for transforming one solution into other and provides a guidance for measuring the attractiveness of theses moves. Example of moves are swapping between two tasks, changing value of a variable (increase, decrease).
A partial list of Tabu Search applications: 1. Employee scheduling 2. Maximum Satisfiability problems 3. Character recognition 4. Space planning and architectural design 5. Telecommunication path assignment 6. Probabilistic logic problem 7. Neural network pattern recognition 8. Machine scheduling 9. Traveling salesman problem 10. Graph coloring
Tabu Search Principles
Tabu Search based on three main concepts: 1. The use of flexible attribute based memory structures, that allows evaluation criteria and historical search information to be exploited move thoroughly than by rigid memory structures or by memory-less systems. 2. A mechanism that evaluate the movement based on a specific criteria in tabu search 3. The use of memory functions of different time spans from short term to long term, to implement strategies for intensify — to focus on a specific region, to diversifications — that drive the search in new regions.
Short term memory and aggressive search
Short term memory in tabu search can be represented as an aggressive exploitation that seeks to make the base move possible. By making a list of candidate moves that can lead to a new solution from the current solution.
Tabu Search provides constrains that prevents repeating of certain moves. By considering those moves as forbidden (Tabu)… (Ahhh that’s why it called Tabu Search!). Tabu Search is intended to prevent cycling back into a local minima, and broadly to introduce the search to follow a new trajectory.
But.. how can Tabu determine the best candidate? Simple!, using the objective function!..
Things are still not clear?! don’t worry I did not understand it also before I saw the following boxed graph:
Selecting the best admissible candidate — taken from [1]
Example time!!!
ِA simple illustration for Tabu Search is the minimum cost spanning tree problem that includes constraints to prevent certain edge from appearing . The problem can be represented by five nodes so the spanning tree consists of four edges and every edge has a cost as illustrated in the image below:
In this problem we need to minimize the cost of connecting the nodes with each other. Every edge is represented here by xi where i=[0..7] and xi can take 0 or 1 (0 the edge does not exists). Every edge has a cost. For example the cost of the initial solution here is 6+2+8+0 = 16 (pretty good huh).
But wait.. don’t forget the other part of the problem, some edges are prohibited to appear.. so lets put some constraints here:
x1 + x2 + x6 ≤ 1
x1 ≤ x3
When we violate those constraints we penalize the cost of 50 for each unit of violation . So in the figure above we have 2 violations so the penalty is 100. and the total cost of that spanning tree is 116 :)
We need to find a solution that gives a low cost without violating the constrains above. To apply Tabu Search we apply swap transform by dropping one edge and add another to transform to another solution.
When we choose to add an edge we must drop another edge in a way that don’t create a cycle. Admissible move is the move that have the lowest cost taking into consideration the violation penalty cost.
Tabu restriction is defined here as the added edge we define as a tabu status. This makes edges that are selected as tabu to not been dropped out of the tree as long as they are tabu. In the example we allow only two edges to be tabu. Which means any added edge remains tabu for two iteration.
The aspiration criteria here is to override a tabu status if the resulting tree is better than the best tree produced so far. We will run the algorithm now for and discuss each iteration. Iterations are represented in figure 1 below:
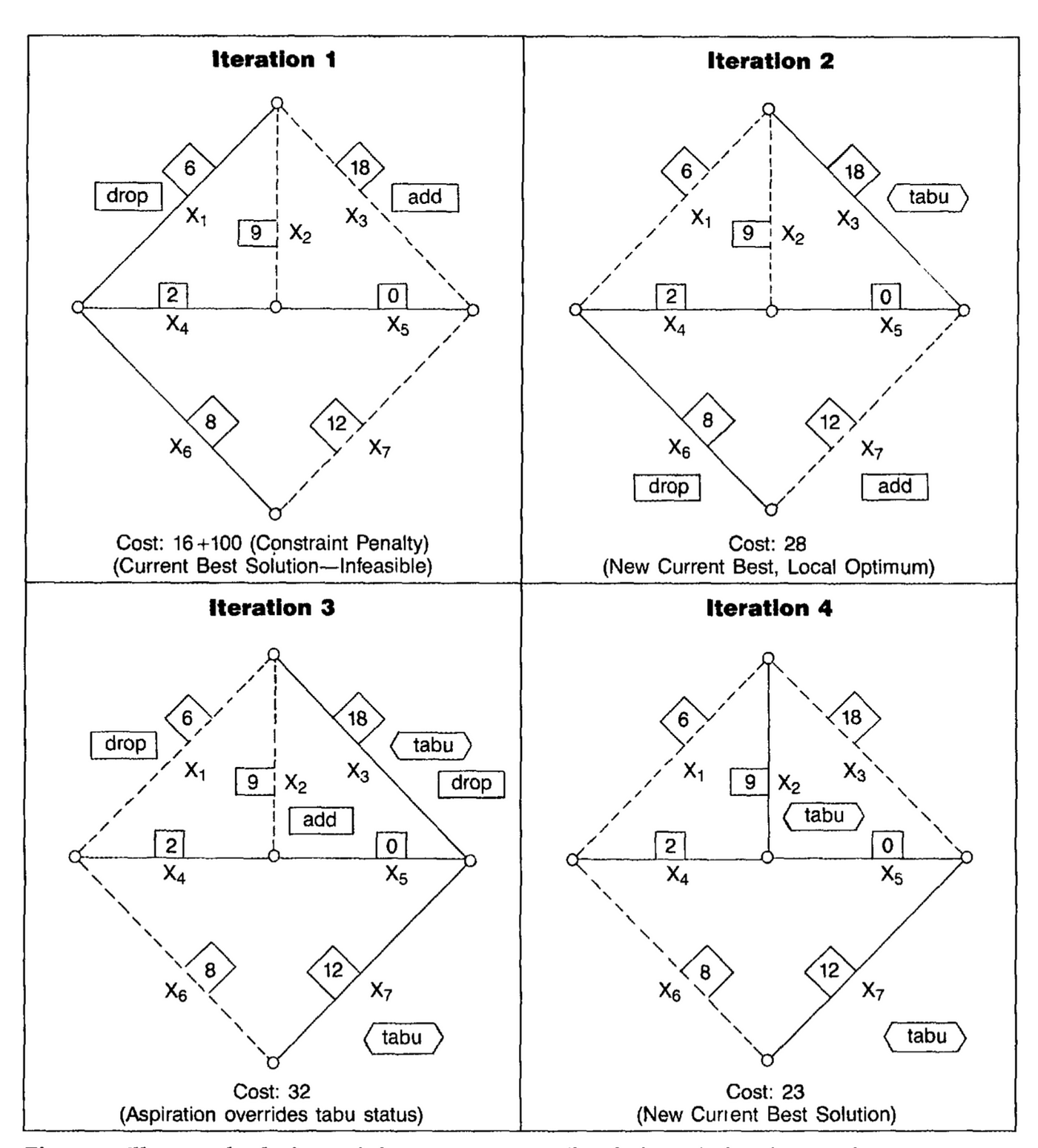
Iteration1: from iteration 1 the best move that we can do in a way not to violate the constrains is by adding x3 and dropping x1. This will reduce the penalty from 100 -> 0. while increasing the cost from 16 -> 28. X3 now is considered as tabu.
Iteration 2: now by the tabu status rule we make x3 as tabu. so we can’t drop x3. From the remaining the best choice is to add x7 and drop x6. Then make x7 as tabu. The chosen move produce worst cost than the previous. Now we have x3, x7 are considered as Tabu. and if we want to make any move we will make the cost worse. so we are in a state that has a bad cost and we can’t make any other move which is called local minimum.
Iteration 3: Now since we reach a local minimum we can override tabu status by adding x2 and drop x3. This move satisfy the aspiration criterion by producing a tree that has a better cost so we make this move.
Iteration 4: X2, X7 are now tabu. The algorithm will continue the moves by adding x3 and dropping X5. X3 and X2 now are tabu
Implementation
I forked an implementation of tabu search in Python and improved it to solve the problem of Traveling Salesman, please feel free to use and modify the code:
"""
This implementation for tabu search is modified from:
https://www.techconductor.com/algorithms/python/Search/Tabu_Search.php
Reference:
https://www.researchgate.net/publication/242527226_Tabu_Search_A_Tutorial
"""
import copy
import math
def distance(point1, point2):
return math.sqrt((point1.x - point2.x)**2 + (point1.y - point2.y)**2)
def generate_neighbours(points):
"""This function geenrates a 2D distance matrix between all points
Parameters
----------
points : type
Description of parameter `points`.
Returns
-------
type
Description of returned object.
"""
dict_of_neighbours = {}
for i in range(len(points)):
for j in range(i+1, len(points)):
if i not in dict_of_neighbours:
dict_of_neighbours[i] = {}
dict_of_neighbours[i][j]= distance(points[i], points[j])
else:
dict_of_neighbours[i][j] = distance(points[i], points[j])
# dict_of_neighbours[i] = sorted(dict_of_neighbours[i].items(), key=lambda kv: kv[1])
if j not in dict_of_neighbours:
dict_of_neighbours[j] = {}
dict_of_neighbours[j][i] = distance(points[j], points[i])
else:
dict_of_neighbours[j][i] = distance(points[j], points[i])
# dict_of_neighbours[i] = sorted(dict_of_neighbours[i].items(), key=lambda kv: kv[1])
return dict_of_neighbours
def generate_first_solution(nodes, dict_of_neighbours):
start_node = nodes[0]
end_node = start_node
first_solution = []
distance = 0
visiting = start_node
pre_node = None
while visiting not in first_solution:
_tmp = copy.deepcopy(dict_of_neighbours[visiting])
_tmp.pop(pre_node, None)
next_node = min(_tmp.items(), key=lambda x: x[1])[0]
distance += dict_of_neighbours[visiting][next_node]
first_solution.append(visiting)
pre_node = visiting
visiting = next_node
first_solution.append(nodes[0])
distance += dict_of_neighbours[pre_node][end_node]
return first_solution, distance
def find_neighborhood(solution, dict_of_neighbours, n_opt=1):
neighborhood_of_solution = []
for n in solution[1:-n_opt]:
idx1 = []
n_index = solution.index(n)
for i in range(n_opt):
idx1.append(n_index+i)
for kn in solution[1:-n_opt]:
idx2 = []
kn_index = solution.index(kn)
for i in range(n_opt):
idx2.append(kn_index+i)
if bool(
set(solution[idx1[0]:(idx1[-1]+1)]) &
set(solution[idx2[0]:(idx2[-1]+1)])):
continue
_tmp = copy.deepcopy(solution)
for i in range(n_opt):
_tmp[idx1[i]] = solution[idx2[i]]
_tmp[idx2[i]] = solution[idx1[i]]
distance = 0
for k in _tmp[:-1]:
next_node = _tmp[_tmp.index(k) + 1]
distance = distance + dict_of_neighbours[k][next_node]
_tmp.append(distance)
if _tmp not in neighborhood_of_solution:
neighborhood_of_solution.append(_tmp)
indexOfLastItemInTheList = len(neighborhood_of_solution[0]) - 1
neighborhood_of_solution.sort(key=lambda x: x[indexOfLastItemInTheList])
return neighborhood_of_solution
def tabu_search(first_solution, distance_of_first_solution, dict_of_neighbours, iters, size, n_opt=1):
count = 1
solution = first_solution
tabu_list = list()
best_cost = distance_of_first_solution
best_solution_ever = solution
while count <= iters:
neighborhood = find_neighborhood(solution, dict_of_neighbours, n_opt=n_opt)
index_of_best_solution = 0
best_solution = neighborhood[index_of_best_solution]
best_cost_index = len(best_solution) - 1
found = False
while found is False:
i = 0
first_exchange_node, second_exchange_node = [], []
n_opt_counter = 0
while i < len(best_solution):
if best_solution[i] != solution[i]:
first_exchange_node.append(best_solution[i])
second_exchange_node.append(solution[i])
n_opt_counter += 1
if n_opt_counter == n_opt:
break
i = i + 1
exchange = first_exchange_node + second_exchange_node
if first_exchange_node + second_exchange_node not in tabu_list and second_exchange_node + first_exchange_node not in tabu_list:
tabu_list.append(exchange)
found = True
solution = best_solution[:-1]
cost = neighborhood[index_of_best_solution][best_cost_index]
if cost < best_cost:
best_cost = cost
best_solution_ever = solution
elif index_of_best_solution < len(neighborhood):
best_solution = neighborhood[index_of_best_solution]
index_of_best_solution = index_of_best_solution + 1
while len(tabu_list) > size:
tabu_list.pop(0)
count = count + 1
best_solution_ever.pop(-1)
return best_solution_ever, best_cost
Conclusion
Tabu search is a meta heuristic search algorithm that utilize the idea of having short term memory to avoid sticking in a local minima. It has been used in many applications one of them is Traveling Salesman Problem. Speaking about TSP it worth to mention that the best reported algorithm to solve it is guided local search algorithm.
References
I used the following reference as the main source of information written in this post (really this is the best resource for tabu search: [1] https://www.researchgate.net/publication/242527226_Tabu_Search_A_Tutorial [2] https://en.wikipedia.org/wiki/Tabu_search [3] http://www.cleveralgorithms.com/nature-inspired/stochastic/tabu_search.html